Как подбросить бутылку так, чтобы она приземлилась на дно? ”water bottle flipp challenge”

Многим уже знакома фишка с тем, что если подбросить бутылку, частично заполненную жидкостью, то она может приземлиться ровно на дно. Это предложили исследовать физикам к предстоящему в 2018 году международному турниру юных физиков, который состоится в Китае. Такие турниры проводятся и в России -
видео демонстрация команды из Барабинска:



В формулировке задачи было задано исследовать явление и параметры, влияющие на удачное приземление бутылки. Полное динамическое описание такой задачи достаточно сложное (видно, что вода внутри перетекает по мере вращения бутылки, изменяя момент инерции, а значит и угловую скорость), но я хочу попытаться дать хотя бы приближённое к действительности простое описание системы.

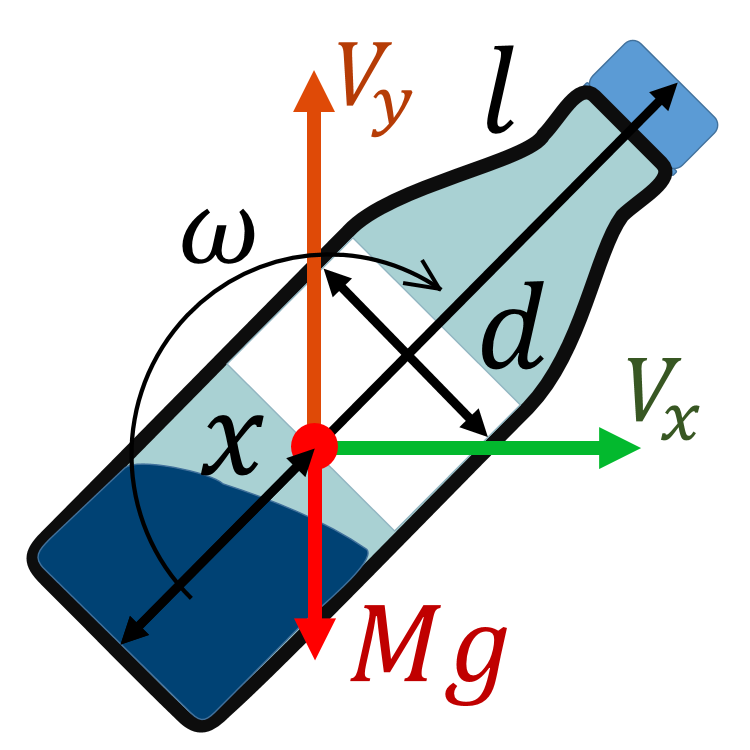
В момент закрутки бутылки вращение происходит относительно горлышка (верхней части бутылки). После того, как бутылку отпускают, она начинает вращаться и двигаться поступательно:

Удобнее рассматривать это вращение относительно оси, проходящей через центр масс (одна из главных осей инерции). Тогда всё движение можно разделять на вращение относительно центра масс и поступательное движение центра масс. Ясно, что горизонтальная скорость не вносит вклад в вероятность успешного приземления: определяющими параметрами будут то, сколько оборотов успевает сделать бутылка до удара (угловая скорость) и время падения, которое определяется начальной высотой и вертикальной скоростью. Горизонтальная скорость влияет только на то, в каком месте бутылка приземлится (нам это не интересно). Тогда для удобства положим горизонтальную скорость равной нулю.
Для начала найдём положение центра масс. Если высота бутылки - \( l \), масса бутылки - \( m_b \), высота уровня жидкости - \( h \) и масса воды - \( m_l \), то считая бутылку равномерным цилиндром получим координату центра масс относительно дна бутылки - \( x \):

$$
x = \frac{m_b l + m_l h}{2(m_b+m_l)} \qquad (1.1)
$$
При этом расстояние от верхней части бутылки до центра масс - \(r = l - x \):

$$
r = \frac{m_b l + m_l (2l - h)}{2(m_b+m_l)} \qquad (1.2)
$$
Теперь, используя (1.2), можно найти начальную вертикальную скорость - \( V_0 \), имея начальную угловую скорость - \( \omega \). Предполагая, что человек отпускает бутылку в момент её горизонтального положения, получим:

$$
V_0 = \omega \frac{m_b l + m_l (2l - h)}{2(m_b+m_l)} \qquad (1.3)
$$
Имея начальное расстояние от центра масс бутылки до пола равное \( H \) и начальную скорость из (1.3), можно найти время падения бутылки (Зная, что конечное расстояние от центра масс до пола должно быть равно \( x \)):

$$
T = \frac{V_0}{g}\Bigg(1 + \sqrt{1 + \frac{2g(H-x)}{V_0^2}} \Bigg) \qquad (1.4)
$$
Подставляя в (1.4) (1.3) и (1.1), получим конечную формулу для времени падения, необходимого для успешного приземления:

\(
T = \omega \frac{m_b l + m_l (2l - h)}{2g(m_b+m_l)} \Bigg( 1 + \sqrt{1+ \frac{8g(m_b+m_l)^2\Bigg( H-\frac{m_b l + m_l h}{2(m_b+m_l)}\Bigg)}{\omega^2(m_b l + m_l (2l - h))^2} }\Bigg) \qquad (1.5)
\)

Формула получилась достаточно большая. Это произошло потому, что время связано с начальной скоростью, которая определяется угловой скоростью и координатой центра масс. В свою очередь, координата центра масс зависит от параметров системы. В таком виде использовать это соотношение не удобно, но нам (1.5) напрямую не понадобится.

Самый главный вопрос - с какой угловой скоростью нужно запустить бутылку при заданных параметрах системы, чтобы она успешно приземлилась? Бутылка за время падения должна сделать \( 3/4 \) оборота то есть повернуться на угол \( \alpha = {3 \pi}/{2} = \omega T \) (рисунок внизу).

Используя то, что \( {3 \pi}/{2} = \omega T \) и (1.4) получим, что

$$
\frac{\omega^2 r}{g} \Bigg( 1 + \sqrt{1 + \frac{2g(H-x)}{\omega^2 r^2}} \Bigg) = \frac{3 \pi}{2} \qquad (1.6)
$$

Решая это уравнение относительно \( \omega \), мы увидим, что единицы из скобки и из корня при возведении в квадрат взаимно уничтожаться и получится совсем простое квадратное уравнение. Мы берём только положительный корень, так как работаем с модулем угловой скорости (направление мы учли при подсчёте угла поворота):

Подставляя (1.1) и (1.2) в (1.7) и учитывая, что \( m_l = \rho_l \pi R^2 h \), где \( \rho_l \) - это плотность залитой жидкости, а \( R \) - это радиус бутылки, получаем конечную формулу для угловой скорости:

$$
\omega = \frac{3\pi}{2} \sqrt{\frac{g(m_b+\rho_l \pi R^2 h)}{m_b(l \lambda_- + 2H) + \rho_l \pi R^2 h(3\pi l + 2H - h \lambda_+)}} \qquad (1.8)
$$
Где \( \lambda_- = \frac{3 \pi}{2} - 1 \); \( \lambda_+ = \frac{3 \pi}{2} + 1 \)

Проще всего использовать (1.7), подставляя заранее рассчитанные по формулам (1.1) и (1.2) \( r \) и \( x \).

Также необходимо учесть ограничения на установку, происходящие из-за того, что бутылка имеет размер и нужно, чтобы когда она сделала оборот на \( \pi / 2 \), расстояние до пола было больше, чем \( r \):

$$
H + \frac{V_0 T}{3} - \frac{gT^2}{18} > r \qquad (1.9)
$$
В противном случае бутылка просто ударится верхней частью о пол.
Используя то, что \( \omega T = {3 \pi}/{2} \), решаем неравенство (1.9) относительно \( \omega \).

Получается, что при увеличении размеров бутылки, необходимая для переворота угловая скорость уменьшается! Почему же так получилось? Дело в том, что в нашем способе бросания время падения определяется начальной вертикальной скоростью, которая в свою очередь определяется угловой скоростью и размерами бутылки: чем больше размер, тем больше \( r \), а значит больше и \( V_0 \)!

Условие (1.10) достаточно легко выполняется практически для любых начальных высот (Это легко понять, сравнивая (1.10) с (1.7)). Проблемы начинаются при отрицательных высотах: на большую возвышенность забросить бутылку не получится (в нашем способе бросания):

Друзья! Я очень благодарен вам за то, что вы интересуетесь моими работами, ведь каждый пост на сайте даётся очень непросто. Я буду рад любому отклику и поддержке с вашей стороны.