Описание движения жесткого шара. Компьютерная симуляция. #1

Как физически и математически описать и смоделировать движение шарика, учитывая возможность его вращения, трение и потери энергии?
Достаточно давно, участвуя в турнире юных физиков, я описал движение упругих и жестких мячиков. Задача заключалась в том, чтобы определить параметры, влияющие на угол отскока, угловую и линейную скорость после удара и потери энергии при деформациях.
Это первая из цикла статей, посвящённых описанию удара.

Кстати, у меня есть замечательная школа математики для программистов – Академия вектозавров. Первую, бесплатную, главу пройти обязательно всем! :)

В этой статье я расскажу, как можно описать удар о жесткую поверхность жёсткого мяча, используя законы ньютона и сохранения импульса. Также я покажу, как можно сделать компьютерную симуляцию мяча, используя полученные результаты. То есть использовать это можно будет и для создания компьютерных игр, где нужно точно описать удар.
Вторая статья будет про движение упругих мячей.
Чтобы представлять себе, что мы получим в итоге, я покажу конечный результат:

Описание движения жесткого шара

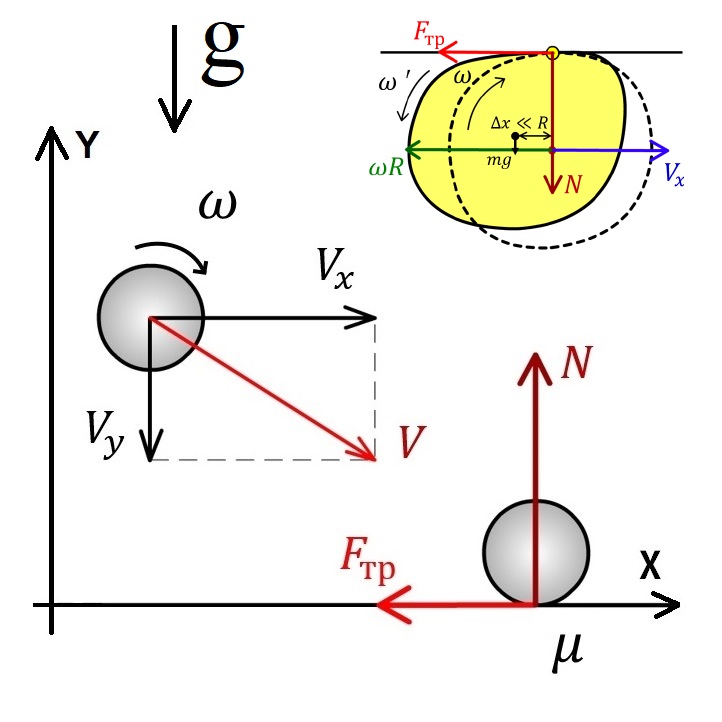
Рассмотрим случай, когда абсолютно жесткий шар (нет деформаций во время удара) массы \(m\) налетает на жесткую плоскость с горизонтальной и вертикальной скоростями \(V_x\) и \(V_y\), угловой скоростью \(\omega\), радиусом \(R\) и коэффициентом трения между поверхностью шара и плоскостью \(\mu\):

Положительное направление угловой скорости показано на рисунке. Ясно, что если мы опишем первый удар, то легко сможем описать и второй.
На рисунке не указана сила тяжести, но её присутствие никак не повлияет, ведь сила реакции опоры во время удара намного больше силы тяжести (сила реакции опоры меняет направление вертикальной скорости, а значит именно она определяющая).

Удар происходит не мгновенно, а длится какое-то конечное время. В это время (когда есть проскальзывание) на шар действует сила трения-скольжения. Она может быть направлена влево или вправо (в зависимости от направления скорости нижней точки шара).

При \(V_x > \omega R\):
$$
F = -\mu N \qquad (1)
$$
При \(V_x < \omega R\):
$$
F = \mu N
$$
Эта сила изменяет горизонтальную составляющую импульса шара:

$$
\Delta{P_x} = -\mu \int{Ndt} \qquad (2)
$$
Возможны два варианта:
1) Проскальзывание длится все время удара.
2) В некоторый момент проскальзывание прекращается, но удар ещё может продолжаться.

Пусть проскальзывание длится все время удара.
Сила реакции опоры изменяет вертикальную составляющую импульса:

$$
\Delta{P_y} = \int{Ndt} \qquad (3)
$$
Отсюда выразим интеграл и подставим его в выражение (2):

$$
\Delta{P_x} = -\mu \Delta{P_y} \qquad (4)
$$
Некоторое количество энергии, естественно, теряется при вертикальных деформациях мяча во время удара, и в выражении для вертикальной скорости после удара должен появиться некоторый безразмерный коэффициент восстановления, который зависел бы от свойств материала шарика:

$$
V_y^{'} = -\gamma V_y
$$
Путем не сложных преобразований, в итоге, получаем горизонтальную и вертикальную скорости после удара:

$$
V_x^{'} = V_x + \mu V_y (1 + \gamma) \qquad (при \; V_x > \omega R)
$$

$$
V_x^{'} = V_x - \mu V_y (1 + \gamma) \qquad (при \; V_x < \omega R) \qquad (5)
$$

$$
V_y^{'} = -\gamma V_y
$$
Когда \(V_x = \omega R\) проскальзывания нет и \(V_x^{'} = V_x\).
При проверке формул учитывайте, что \(V_y\) всегда отрицательна.

Помимо того, что сила трения изменяет горизонтальную скорость, она ещё меняет угловую. Запишем 2-й закон Ньютона для вращательного движения:

$$
\int{Id\omega} = \mu R \int{Ndt} \qquad (при \; V_x > \omega R)
$$

$$
\int{Id\omega} = -\mu R \int{Ndt} \qquad (при \; V_x < \omega R) \qquad (6)
$$
То есть момент определяет сила трения, плечо которой \(=R\). Момент силы реакции опоры равен нулю из-за нулевого плеча.
В (6) \(I\) - это момент инерции шара, который удобнее записывать как \(I = \alpha mR^2\). Пользуясь этой заменой, уравнением (3) и (6) находим угловую скорость после удара:

$$
\omega^{'} = \omega - \frac{\mu V_y (1 + \gamma)}{R \alpha} \qquad (при \; V_x > \omega R)
$$

$$
\omega^{'} = \omega + \frac{\mu V_y (1 + \gamma)}{R \alpha} \qquad (при \; V_x < \omega R) \qquad (7)
$$
При \(V_x = \omega R\) проскальзывания нет и \(\omega^{'} = \omega\).
Легко получить, что для полного шара \(\alpha = 2/5\), для сферы \(\alpha = 2/3\), для обруча \(\alpha = 1\). (см. Момент инерции)

Мы рассмотрели случай, когда проскальзывание длится все время удара, но как было сказано ранее, возможна такая ситуация, когда проскальзывание прекратилось, но удар ещё продолжается. Рассмотрим и этот случай.

Пусть в некоторый момент устанавливается режим не проскальзывания.
Теперь нельзя как раньше связать (2) и (3), ведь пределы интегрирования будут разными: горизонтальная и угловая скорости остаются постоянными, когда нет проскальзывания (считаем, что нет силы трения-качения), а вертикальная скорость продолжает изменяться!
Если проскальзывание прекратилось, то скорость нижней точки шара равна нулю. В скалярном виде получаем условие движения без проскальзывания: \(V_x^{'} - \omega^{'} R = 0\)
Это условие дает возможность разрешить систему.
Используя это условие и уравнения (2) и (6), получаем угловую и поступательную скорости после удара:

$$
V_x^{'} = \frac{\alpha \omega R + V_x}{1 + \alpha}
$$

$$
V_y^{'} = -\gamma V_y \qquad (8)
$$

$$
\omega^{'} = \frac{\alpha \omega R + V_x}{R(1 + \alpha)}
$$
Легко убедится, что такое решение будет верным и при \(V_x > \omega R\), и при \(V_x < \omega R\) (В первом случае сила трения создаёт положительный момент и в уравнение (6) войдёт со знаком плюс, но эта сила будет уменьшать импульс тела (2), а значит изменение импульса войдет в уравнение со знаком минус. В итоге в правой части получим знак минус. Во втором случае сила трения создаёт уже отрицательный момент, но увеличивает импульс, т.е знак тоже отрицательный.

Из этого решения мы видим, что при \(V_x = \omega R\) угловая и горизонтальная скорости не изменяются, что и следовало ожидать.

Теперь объединим (5), (7) и (8), рассмотрев критический случай, при котором будет выполнятся и первое, и второе решение и получим условие на \(\mu\):

$$
\mu = -\frac{\alpha (V_x - \omega R)}{V_y(1 + \gamma)(1 + \alpha)} \qquad (при \; V_x > \omega R)
$$

$$
\mu = -\frac{\alpha (\omega R - V_x)}{V_y(1 + \gamma)(1 + \alpha)} \qquad(при \; V_x < \omega R) \qquad (9)
$$
Не нужно смущаться минуса перед дробью. Он происходит оттого, что \(V_y\) всегда отрицательна (Шар налетает на плоскость, а значит его скорость направлена против нормали к поверхности)
Очевидно, что при меньшем значении \(\mu\) будет выполнятся первое решение, а при большем - второе. Маленькая сила трения не сможет остановить шарик и проскальзывание будет происходить весь удар. Бóльшая же сила трения быстро остановит шар и мы попадём в режим не проскальзывания.
Видно, что если скорость \((V_x - \omega R)\) точки контакта большая, то скольжение будет происходить весь удар. При малой же скорости условие на \(\mu\) легко выполняется и происходит зацеп.
Обозначим переходную силу трения за \(\mu_{e}\):

$$
\mu_{e} = -\frac{\alpha |V_x - \omega R|}{V_y(1 + \gamma)(1 + \alpha)} \qquad (10)
$$
В случае, когда \(\mu = \mu_{e}\) проскальзывание заканчивается ровно в момент отскока шарика. То есть выполняются оба решения.
Для удобства введем функцию \(\xi(V_x, \omega)\) следующим образом:

$$
\xi(V_x, \omega) =
\begin{bmatrix}
1 \; при \; V_x > \omega R\\
-1 \; при \; V_x < \omega R\\
\end{bmatrix}
$$
В конечном итоге получаем решение:

Угол отскока легко найти зная горизонтальную и вертикальную скорость после удара:

$$
\tan \phi = \frac{V_x^{'}}{V_y^{'}}
$$
Где \(\phi\) - угол между вектором скорости после удара и вертикалью.

Как видно, ответ получился достаточно громоздким. Но это только из-за того, что помимо двух случаев проскальзывания возможны два направления силы трения, каждое из которых мы учли при решении.

Удар как линейное преобразование.

Теперь моя любимая часть :)
Представим себе, что шар налетает не на горизонтальную поверхность, а на наклонённую под углом \(\varphi\) плоскость. В этом случае нам нужно просто спроецировать скорости \(V_x\) и \(V_y\) на новые оси (совершить поворот координат на угол \(\varphi\)):

Записывается такое преобразование очень просто:

$$
\begin{pmatrix}
v_x \\
v_y \\
\Omega
\end{pmatrix}
=
\begin{bmatrix}
cos\varphi & sin\varphi & 0 \\
-sin\varphi & cos\varphi & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{pmatrix}
V_x \\
V_y \\
\omega
\end{pmatrix}
=
T^{-1}
\begin{pmatrix}
V_x \\
V_y \\
\omega
\end{pmatrix}
\qquad (11)
$$
После перехода (11) нужно найти скорости после удара и вернуться в старую систему координат.
Заметим, что наше решение (для скоростей после удара) является линейным преобразованием скоростей (когда я это заметил у меня пошли мурашки по коже. Такое бывает и это нормально). То есть удар является линейным преобразованием!

$$
\begin{pmatrix}
V_x^{'} \\
V_y^{'} \\
\omega^{'}
\end{pmatrix}
=
TPT^{-1}
\begin{pmatrix}
V_x \\
V_y \\
\omega
\end{pmatrix} \qquad (12)
$$
Единственное, что немного портит картину, так это условие на \(\mu_e\) и функция \(\xi(V_x, \omega)\), ведь для нахождения линейного преобразования \(P\) нужно проверить выполнимость всех условий и выбрать подходящий ответ:

Компьютерное моделирование движения

Ну а теперь самое интересное - результат работы алгоритма!
Имея угловую и поступательную скорость до удара, можно предсказать что будет после. Для визуализации движения и проверки полученных результатов неплохо бы сделать моделирование. О том, как численно решать задачи я уже упоминал в одной из моих статей. Я накидал простой алгоритм для лучшего понимания того, как это все можно реализовать:

Ну и, наконец, результат работы программы!
В данном случае мы запускаем шар между двумя горизонтальными пластинами:

Данная постановка легко повторяется в реальной жизни. Для проверки я собрал вот такую установку:

Траекторию мячика я брал из видео с помощью специальной программы для трассировки.

Как видно модель хорошо согласуется с экспериментом!
А вот что будет если бросить шарик на наклонную поверхность:

Алгоритм работает и в сложных случаях, какой был показан в самом начале:

Если трение не велико, то возможно прокручивание и изменение направления скорости:

В следующей статье я расскажу, как можно описывать движение не жёстких шариков, а упругих мячей. С упругими мячиками можно получить много интересных траекторий. Например вот такую:

Друзья! Я очень благодарен вам за то, что вы интересуетесь моими работами, ведь каждый пост на сайте даётся очень непросто. Я буду рад любому отклику и поддержке с вашей стороны.