Saxon Bowl IYPT 2020 - analytical solution from ilinblog (Саксонская миска)

Today I will tell you about my vision on the problem #6 "Saxon Bowl" IYPT 2020.
Due-to I have a lot of english IYPT players last year whose used my website, I decided to choose English for this article.

Nevertheless, I had Russian users and I think it will be a good practice to learn the language!

But before you dive in I feel like a warning is in order. I am not a proffesional physicist and I am absolutely sure that even in this article I have a lot of possibe mistakes. Before using this it will be nice to check all results with your teachers. I appreciate any corrections in comments from you.

It's good to start with the problem' statement:
A bowl with a hole in its base will sink when placed in water.
The Saxons used this device for timing purposes. Investigate
the parameters that determine the time of sinking.

As I understand, we can measure the elapsed time, knowing water level in the bowl. Therefore, our goal is to find the dependence of water level from time.

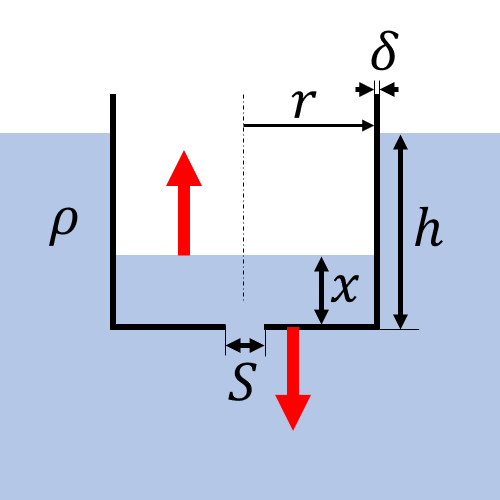
Essentially we have a bowl with a hole on the surface of the water. Let's consider this system:

I assume that h(t) is a constant quantity. Furthermore, I will not consider сapillary action. I believe that only difference of pressure influences the result.

In our particular case I decide to solve this problem, using dynamic consideration. (Or the same, second Newton law)
As I mentioned before the major effect is difference in pressure. Let's consider this difference:

On the small piece of water coming inside acts pressure-gradient force:

$$
F = \Delta P \cdot S = m \cdot a \qquad (1)
$$
We can calculate mass, knowing the water density and the volume of the piece:

$$
m = S \cdot \delta \cdot \rho
$$
Now we can rewrite (1) as

$$
S \delta \rho \cdot \ddot{y} = \Delta P \cdot S = \rho g S \cdot (h - x),
$$
where \(x\) - water level inside the bowl and \(y\) - piece of water position.

Finally, we have following expression:

$$
\ddot{y} = \frac{g}{\delta} \cdot (h - x) \qquad (2)
$$

We can't solve this, because there are two unknown variables. We should link \(x\) with \(y\).
We can easy do this, using the fact water is not compressible fluid:

$$
\dot{y} \cdot S = \dot{x} \cdot \pi r^2, \qquad (3)
$$
where \(r\) - radius of the bowl.

Differentiating (3), we get:

$$
\ddot{y} \cdot S = \ddot{x} \cdot \pi r^2 \qquad (4)
$$
Using (4) and (2) we have the following inhomogeneous differential equation:

$$
\ddot{x} + \frac{gS}{\delta \pi r^2}x = \frac{gSh}{\delta \pi r^2} \qquad (5)
$$
"The solutions of any linear ordinary differential equation of any order may be deduced by integration from the solution of the homogeneous equation obtained by removing the constant term."

As we know, solution of inhomogeneous differential equation can be found as sum of general solution of homogeneous equation and particular solution of inhomogeneous equation.

General solution of homogeneous

Characteristic polynomial for our equation is:

$$
{\lambda}^2 + \frac{gS}{\delta \pi r^2} = 0
$$
hence, \(\lambda = \pm \sqrt{\frac{gS}{\delta \pi r^2}}\)

Therefore, general solution we can express by following way:

$$
x_{gh} = Ae^{i\sqrt{\frac{gS}{\delta \pi r^2}}t} + Be^{-i\sqrt{\frac{gS}{\delta \pi r^2}}t}
$$

Particular solution of inhomogeneous

We can make sure that solution is \(x_{pi} = h\) by substracting in (5)

General solution of inhomogeneous

$$
x_g = Ae^{i\sqrt{\frac{gS}{\delta \pi r^2}}t} + Be^{-i\sqrt{\frac{gS}{\delta \pi r^2}}t} + h \qquad (6)
$$
With initial conditions:

$$
x(0) = 0 \Rightarrow A+B+h=0 \qquad (7)
$$
$$
\dot{x}(0) = 0 \Rightarrow A-B=0 \qquad (8)
$$

Combining (6), (7) and (8) we can get:

$$
x = 2 h sin^2{ \left( \sqrt{\frac{gS}{\delta \pi r^2}} \frac{t}{2} \right) }
$$
From this formula we can conclude, that initial velocity \(\dot{x}\) is small due-to second initial condition (water is not yet in motion).
Also, we can clearly see that final velocity becomes very small. It happens because difference in pressure becomes very small, so force, acting on a small piece of water, becomes very small:

We should understand that we are interested in area, where \(x \leq h\) due-to after that your bowl is flooded.

In addition we can get expression for the time of flooding (\(x = h\)):

$$
T \approx \frac{\pi r}{2} \sqrt{\frac{\delta \pi}{gS}}
$$
Finally, I would like to convey to you an important idea. As I mentioned in the beginning of the article, this small part of solution should not be absolutely right: you have to check all information you found in the internet and make your own general point of view. This is basic idea of IYPT. Good luck!

Друзья! Я очень благодарен вам за то, что вы интересуетесь моими работами, ведь каждый пост на сайте даётся очень непросто. Я буду рад любому отклику и поддержке с вашей стороны.