Закон электромагнитной индукции. (Закон Фарадея)

Сегодня мы разберёмся с одним из самых главных и интересных законов электродинамики – законом Фарадея.

Разберёмся как работает магнитная левитация и узнаем, как в Китае изобрели поезд, способный разгонятся до пятисот километров в час.

Приятного чтения!

Кстати, у меня есть замечательная школа математики для программистов – Академия вектозавров. Первую, бесплатную, главу пройти обязательно всем! :)



Я думаю, что большинству смотрящих уже знакомо понятие магнитного поля. А если не знакома, то вкратце магнитное поле можно описать как силовое поле, действующее на движущиеся электрические заряды.

$$
F = q [V \times B] \qquad (1)
$$

Для начала следует уяснить тот факт, что при протекании тока по проводу, создаётся магнитное поле, которое кольцами окружает проводник.

Это поле можно посчитать в любой точке (Закон Био-Савара-Лапласа):

$$
B = \frac{\mu_0}{4\pi} \int_{\gamma}{\frac{I[dr\times (r_0-r)]}{(r_0-r)^3}} \qquad (2)
$$

То есть магнитное поле можно создать с помощью проводника с током, ну или используя обычный постоянный магнит.

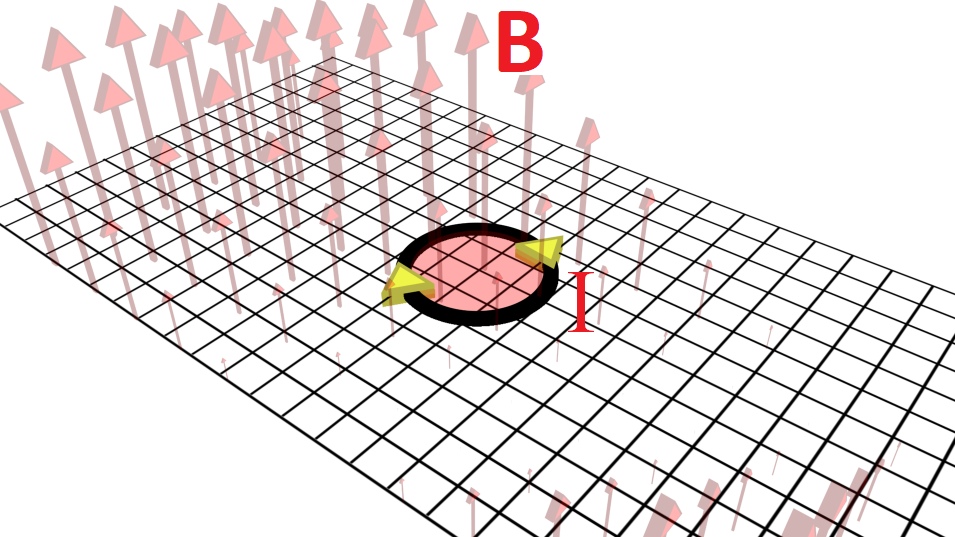
А теперь представьте, что у нас есть кусочек провода, по которому не идёт ток, ведь он ни с чем не соединён. Этот кусок мы замкнём, получив при этом колечко.

Теперь самое главное: в чем собственно суть закона Фарадея.
Что будет, если это колечко мы поместим в переменное магнитное поле. Может показаться странным, но по этому колечку начнёт течь ток. Без всяких источников тока, аккумуляторов и так далее.

Когда мы услышали этот факт, становится понятно, с чем нужно разобраться в первую очередь:
1) Почему вообще появляется напряжение в колечке и зачем для этого именно переменное магнитное поле?
2) Какая величина напряжения образуется в кольце. Ведь зная этот факт, можно уже размышлять о том, как его использовать. Например, для зажигания лампочки или для работы компьютера.

На оба эти вопроса можно ответить с помощью закона Фарадея.

Закон Фарадея утверждает, что напряжение, образующегося в колечке, пропорционально скорости изменения потока магнитного поля через это кольцо, взятое с обратным знаком.

$$
\varepsilon = -\frac{d\Phi}{dt} \qquad (3)
$$
Давайте по отдельности разберём каждое слагаемое в этом законе.

Первое (\(\varepsilon\)) — это напряжение тока. Ещё его называют ЭДС индукции. ЭДС расшифровывается как Электро-Движущая Сила. Из-за этого напряжения возникает ток в колечке. Тут всё ясно.

Второе – это магнитный поток. О котором я сейчас расскажу.
Но в этой формуле важен не сам поток ФИ, а его производная по времени.

Теперь про поток. Что это вообще такое?
Поток в физическом смысле очень схож с тем, что мы понимаем под потоком. Для того, чтобы было легче понять смысл этой величины, рассмотрим протекание воды в трубе.

Потоком мы называем обьем воды, вытекающей в единицу времени. То есть чем больше объёма воды вытекает за одно и то же время, тем больше поток.
Если вода имеет скорость V, то изменение объема равно площади сечения трубы, умноженной на изменение координаты воды. То есть поток получился равным \(\Phi = SV\).

Как мы и говорили, чем больше скорость воды в трубе, тем больше поток.
Теперь вернёмся к нашей теме. Поток магнитного поля очень похож на поток воды, только с той разницей, что у магнитного поля нет понятия скорости частиц.

В простейшем случае, магнитный поток – это величина магнитного поля, умноженная на площадь нашего контура.

$$
\Phi = BS
$$
Но на самом деле контур может быть не совсем круглым, а поток можно считать по любой поверхности, краем которой является этот контур.
При этом сам поток из-за этого не изменится несмотря на то, что площадь поверхности может сильно возрастать.

В этом случае нужно считать скалярное произведение вектора нормали и поля в каждой точке. Я не буду рассказывать очень подробно о том, как следует считать поток магнитного поля в произвольном случае и со сложной формой проводника.
Основная идея – это разбить контур на небольшие части, в которых магнитное поле не зависит от координаты и просуммировать скалярные произведения магнитного поля и вектора нормали.

$$
\Phi = \int_{\partial{M}}{(\vec{B}\cdot d\vec{S})}
$$
В уравнении Фарадея нас интересует не поток, а именно его изменение. Ведь было бы слишком просто создать постоянное магнитное поле (обычным магнитиком) и получить при этом бесплатный вечный ток в колечке.
Для получения тока мы должны менять поток со временем и чем быстрее мы будем это делать, тем больший будет образовываться ток.

Последнее с чем нужно разобраться – это минус в уравнении. На самом деле это очень важная часть.
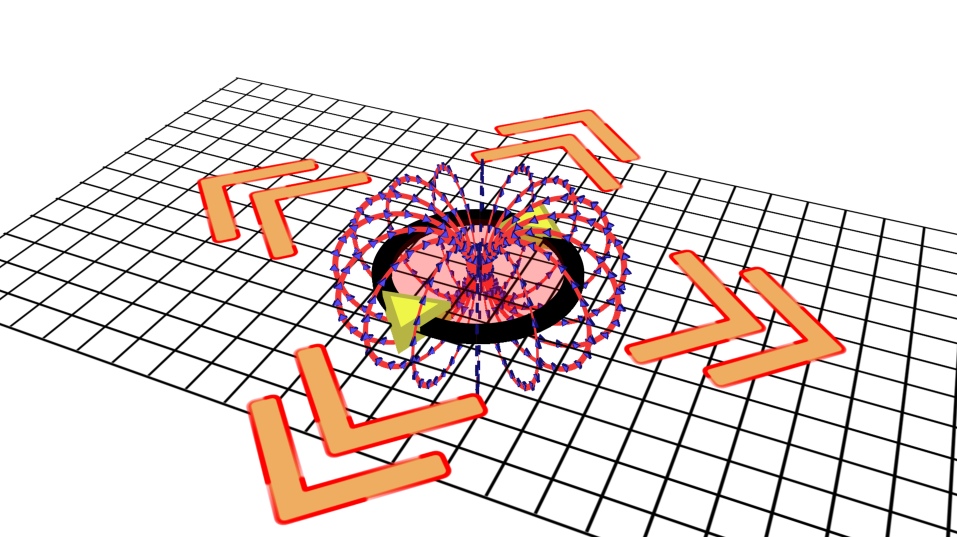
Помните в начале я говорил о том, что ток порождает кольцевое магнитное поле? Так вот и этот случай не исключение.

Мы уже поняли, что переменное магнитное поле создает ток в контуре. Этот ток создаёт кольцевое магнитное поле.
Минус перед производной сигнализирует о том, что создаваемое магнитное поле будет направлено против потока магнитного поля.
По сути, это значит, что при изменении магнитного поля через контур, в последнем создаётся такой ток, который создаёт противоположно направленный поток. То есть контур не дает нам так просто резко увеличить поток, создавая сопротивление.
Тут работает аналогия с движением. Если массивное тело движется, то просто так его остановить не получится: придётся подействовать большой силой.

Можно смотреть на закон Фарадея под таким углом: контур сопротивляется изменению потока и когда мы меняем поток, в контуре возникает ток, чтобы не дать это сделать.
То есть ток возникает не из-за изменения потока, а из-за того, чтобы попытаться сохранить прежний поток.
Контур для уменьшения или увеличения потока через себя может так же деформироваться.
Представим, что по в катушке индуктивности циркулировал большой ток. Теперь если резко отключить ток, то исчезнет индуцируемое магнитное поле и магнитный поток начнёт резко уменьшаться.

Чтобы его сохранить катушка должна создать ток, но его недостаточно. Вдобавок она начнёт разрываться. Ведь при увеличении площади увеличивается поток.
Поэтому при резком выключении тока некоторые электроприборы, в которых используются катушки индуктивности могут даже взорваться.
Год назад в своей курсовой работе я проводил опыты с большими токами и магнитными полями. Суть была в том, что мы пытались с помощью магнитного поля разогнать железный снаряд до огромных скоростей. Токи в цепи при этом были такие большие, что катушку индуктивности просто разрывало на части и для нового эксперимента приходилось заново её изготавливать.

С законом Фарадея связано очень много зрелищных и красивое явлений. Например, левитация сверхпроводника. Левитацию впервые наблюдали в 1933 году. Тогда ученые заметили, что при сильном охлаждении сопротивление некоторых материалов падает до нуля. Самое удивительное то, что сопротивление действительно ноль, не какая-то там маленькая величина, которой можно пренебречь, а прям в точности ноль.



А из закона ома мы знаем, что протекающий в контуре ток равен падению напряжения делённое на сопротивление. Если сопротивление стремится к нулю, то ток стремится к бесконечности, а такого быть не может. Ток если и есть, то он должен быть конечный. Значит напряжение должно быть в точности ноль. А мы выяснили, что напряжение пропорционально изменению потока магнитного поля. Все это значит, что поток магнитного поля у сверхпроводника изменится не может никак.

Происходит вмораживание магнитного потока. Если сверхпроводник находится в магнитном поле, то его положение, очевидно, будет устойчивым.

Левитацию можно устроить и без сверхпроводника. Закон Фарадея – очень мощный закон, позволяющий, играя с индуцирующимися полями, достичь очень неожиданных результатов. Вот, например, машина, которую показывал Veritasium.



Эта громадина запросто левитирует с помощью быстро вращающихся магнитов. Сам ты её вряд ли поднимешь, а вот она тебя запросто.

Сверхбыстрые поезда, изобретённые в Китае, разгоняются до пятисот километров в час. Это стало возможно благодаря закону Фарадея. В таких поездах огромными токами индуцируются гигантские магнитные поля, на этих полях, как на подушке, движется целый поезд. Такая конструкция позволяет не терять много тепла на трение и эффективно разгонятся.



Однако и здесь есть свои нюансы. Например – токи Фуко, возникающие из-за индукции, сильно нагревают проводник и являются одним из основных источников потерь.

Друзья! Я очень благодарен вам за то, что вы интересуетесь моими работами, ведь каждый пост на сайте даётся очень непросто. Я буду рад любому отклику и поддержке с вашей стороны.