Фракталы, DLA кластеры и случайные блуждания

Еще очень давно мне стала интересна тема фракталов, по крайней мере потому что выглядят они очень красиво. Учась на втором семестре ФФ НГУ, я делал лабораторную работу про броуновское движение, в которой столкнулся с фракталами и решил получше в них разобраться. В данной статье я хочу простыми словами поделиться тем, что я узнал и сделал сам.

Кстати, у меня есть замечательная школа математики для программистов – Академия вектозавров. Первую, бесплатную, главу пройти обязательно всем! :)





По википедии: Фрактал - множество, обладающее свойством самоподобия (объект, в точности или приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей).

Приведём простые примеры фракталов:
Множество Кантора. Строится такое множество очень просто: берём отрезок и делим его на три равные части. Среднюю часть выкидываем, а с получившимися боковыми проделываем то же самое. В итоге получится следующая картина:

Другой пример - треугольник Серпинского, который будем строить так: на каждой стороне треугольника отметим середину. По получившимся трём точкам строим треугольник. В итоге получается четыре маленьких треугольника одного размера (внешний исходный не считаем), из которых треугольник в середине мы не трогаем, а с остальными тремя треугольниками проделываем то же самое:

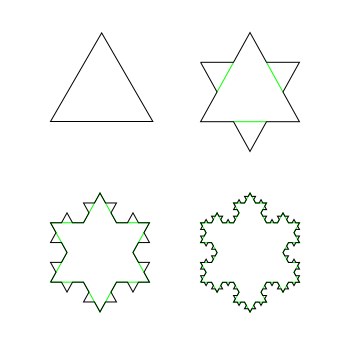
И, наконец, снежинка Коха, которая строится следующим образом: берём отрезок, делим его на три части. Боковые две части не трогаем, а середину заменяем равносторонним треугольником:

Масштабируя части снежинки мы будем получать весь фрактал целиком:

Тот же самый фрактал, только уже в пространстве:

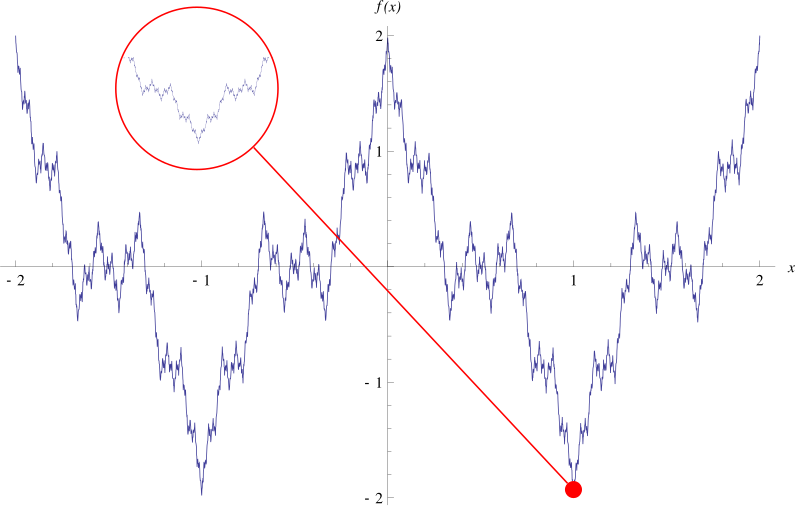
Функция Вейерштрасса — пример непрерывной функции, нигде не имеющей производной. Такая функция тоже самоподобна и задаётся следующим образом:

Где \( a \) — произвольное нечётное число, не равное единице, а \( b \) — положительное число, меньшее единицы. Этот функциональный ряд мажорируется сходящимся числовым рядом \( \sum\limits_{n=0}^{\infty}{b^n} \) поэтому функция \( f(x) \) определена и непрерывна при всех вещественных \( x \):

Есть более сложные фракталы, такие как множество Мандельброта или множество Жюлиа, которые строятся накладыванием некоторых условий на числа комплексной плоскости:

Фрактал - математическая абстракция, являющаяся приближением к тому, что мы видим в реальной жизни. В реальности все ещё интереснее.
Вот, например, кочан капусты:

Или вот вам береговая линия:

Коралл:

Горный хребет:

Облака:

Вот такая вот реальность.

Одна из главных характеристик фракталов является размерность.
Пусть имеется \( n \) мерное множество (\( n \) степеней свободы для координат). Его размерность можно определить следующим образом (размерность Минковского):

Где \( N(\varepsilon) \) - минимальное количество шаров радиуса \( \varepsilon \), необходимое для полного покрытия множества.
Есть похожие равносильные определения размерности (например размерность Хаусдорфа), но размерность Минковского удобна тем, что её можно вычислять итерационно на компьютере. По поводу того, как это делается есть хорошая статья на Хабре.

Легко убедиться, что размерность, определённая таким образом совпадает с тем, что мы понимаем под размерностью обычных тел. Например размерность квадрата равна 2. Действительно, будем покрывать квадрат со стороной \( l \) квадратными шарами радиуса \( \varepsilon \). Ясно, что чтобы полностью покрыть квадрат нам потребуется \( N = ( l/2\varepsilon)^2\) шаров.

Тогда

Для линии размерность получается равной 1:

У фракталов размерность, как правило, дробная. Для вычисления размерности фрактала нужно разрезать все пространство на квадраты радиуса \( \varepsilon \) (кубы) и считать количество квадратов, в которые попадает исследуемое множество. Если провести вычисление \( N(\varepsilon) \) при разных \( \varepsilon \), то можно с высокой точностью найти размерность, как коэффициент наклона аппроксимирующей прямой зависимости \( ln(N(\varepsilon)) \) от \( ln(1/\varepsilon) \).
Например у множества Кантора размерность равна 1. У треугольника Серпинского \( \approx 1.585 \), а у снежинки Коха \( \approx 1.26 \)
Размерность характеризует плотность самоподобия: чем больше плотность, тем ближе объект к двумерному (трехмерному).
Рассмотрим некоторые частные случаи фракталов.

Броуновское движение
Броуновское движение – это беспорядочное тепловое движение малых частиц, взвешенных в жидкости или газе. Открыто в 1827 г. Р. Броуном как движение цветочной пыльцы (частиц с размером \( \sim 1 \) мкм) в воде, видимое при сильном увеличении. Беспорядочное движение частиц обуславливается флуктуациями передаваемого со стороны других частиц импульса. Направление движения постоянно меняется из-за столкновений с другими частицами. Для молекулы воздуха частота столкножений (при нормальных условиях) \( f \approx 0,8 \cdot 10^{10} \) Гц. Для броуновской частицы частота еще больше. В итоге мы имеем просто колоссальное число столкновений.

Такое количество столкновений приводит к сложностям при описании движения частиц реального газа, ведь для полного описания системы нужно знать скорости и координаты всех частиц в каждый момент времени, а также учитывать взаимодействия между ними. Даже имея доступ к самому мощному компьютеру на земле, ученым бы потребовались миллионы лет симуляции нескольких секунд поведения газа. Однако эксперимент показывает, что систему, находящуюся в равновесии можно описать двумя параметрами, считая, что каждая частичка движется абсолютно случайно в каждый момент времени.

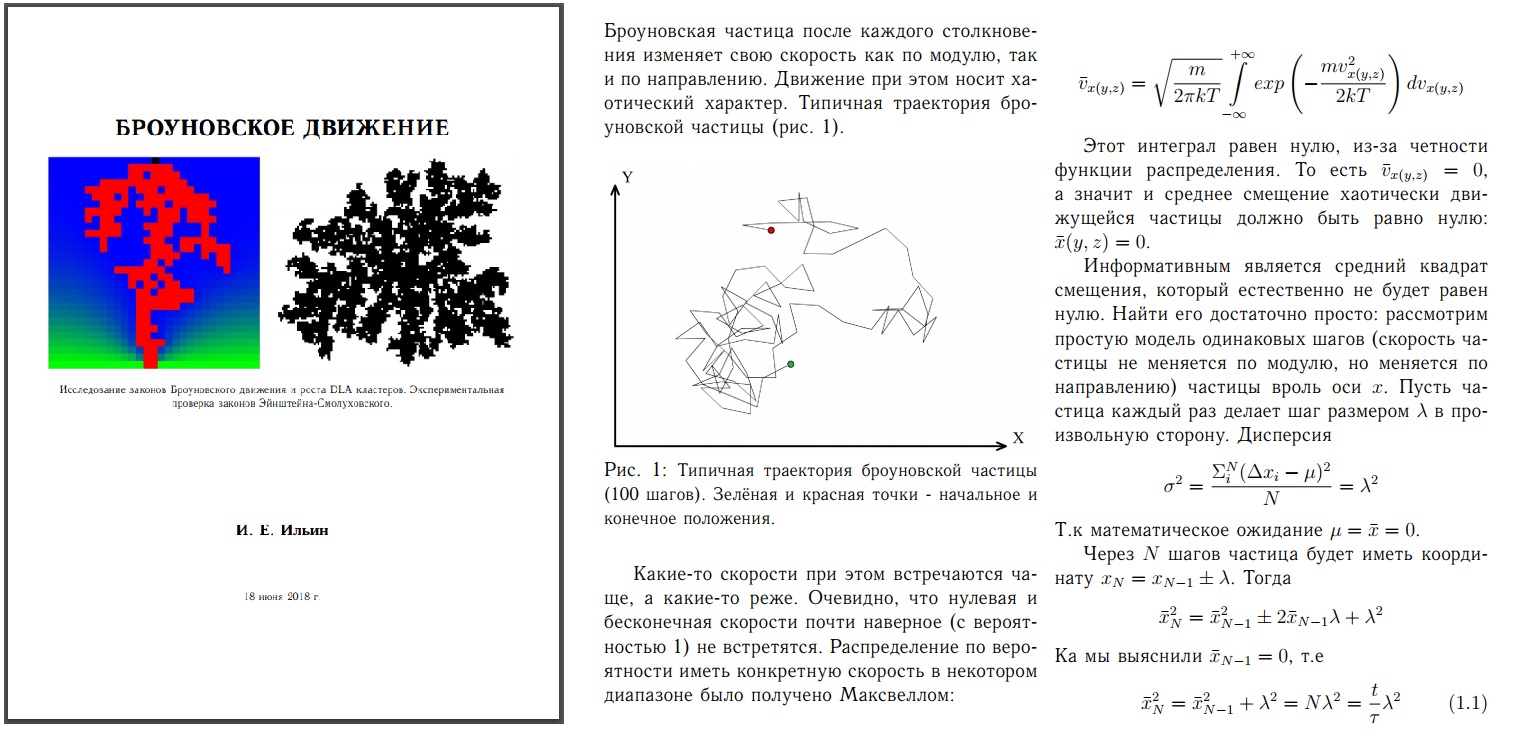
Смоделировать броуновское движение на компьютере достаточно просто: частицу нужно смещать на заданное расстояние (в моделе одинаковых шагов) в произвольном направлении. В двумерном случае это делается выбором произвольного угла \( \phi \in [0; 2\pi] \), например так: \( \phi = random()\cdot2\pi \);
При большом количестве шагов получается следующая картина:

Случайные блуждания частицы можно описать как винеровский случайный процесс. В таком процессе исчезает понятие свободного пробега, в течение которого движение отдельной молекулы существенным образом равномерно и прямолинейно, каждая молекула за конечное время пробегает бесконечный путь, а любая из ее координат есть функция, не имеющая производной и принимающая бесконечное число раз максимальные и минимальные значения в любом интервале.
Траектория движения частицы в таком процессе самоподобна. Демонстрация масштабной инвариантности винеровского процесса:

Пусть частица продиффундировала на расстояние \( R \) и \( \varepsilon \) - длинна одного шага. Т.к \( R^2 \sim \) количеству шагов, то \( N \approx R^2/\varepsilon^2 \). Тогда размерность броуновского движения

При хаотическом движении, частицы, случайно блуждая в веществе, могут встречаться и прилипать друг к другу. В результате этого процесса могут получаться достаточно большие структуры, образование которых мы рассмотрим в следующем пункте:

DLA кластеры, химическая агрегация
Интересным примером фракталов является DLA кластер (Diffusion-limited aggregation), рост которого вызван слипанием свободно блуждающих частиц.
Немного изменим программу из предыдущей части: сделаем так, чтобы частица могла блуждать не в произвольном направлении, а в одном из четырёх (сеточная структура поля). В центр поля поместим затравочную частицу (на неё будут налипать другие частицы в самом начале) и выпустим с произвольного положения частицу, которая прилипнет к кристаллу, если окажется рядом. После прилипания повторяем процедуру: заново выпускаем БЧ и ждём, пока она не прилипнет:

Эффективнее при проверке прилипания проверять не весь кристалл, а только ближайшие частицы и выпускать новые частицы с некоторого эффективного радиуса, который немного больше размера кристалла: это сильно ускорит рост (Поначалу я сделал не так и проверял весь кристалл. Программа при этом работала очень медленно и кристаллы получались очень маленькими и не интересными). Процесс прилипания я анимировал:

Если пропускать промежуточные шаги, то рост кристалла будет происходить примерно так. Обратите внимание на то, как изменяется эффективный радиус:

После некоторого времени роста получается вот такая красивая структура:

Расчеты на компьютере показывают, что размерность такого фрактала \( \approx 1.71 \)
Можно добавить вероятность прилипания, которая будет определятся количеством соседних частиц. В этом случае получится так называемая химическая агрегация. Кристалл в таком случае получается более плотным. Т.е его размерность увеличивается:

На первый взгляд это обычный кластер, но если хорошо присмотреться, то можно увидеть много чего интересного. Вот, что мне удалось в нем разглядеть:

Рост более плотного кристалла:

Если варьировать вероятность то можно получать ещё более плотные кристаллы:

Обратите внимание на образующиеся в процессе роста пустоты в кристалле. Как и следует ожидать, размер этих пустот уменьшается с увеличением плотности кластера.
А вот кластер DLA, выращенный из раствора сульфата меди в ячейке электроосаждения - это реальный эксперимент:

И это очень похоже на компьютерные кластеры!

Симуляция коронного разряда
Коронный разряд - очень красивое явление, которое тоже является фракталом!

В двумерном случае имеем заданное в каждой точке электрическое поле, будем считать, что бездивергентное, и скалярный потенциал. Пусть также свободных зарядов нигде нет, тогда из уравнения Макселла для индукции, используя обобщенную формулу Стокса, поток через любою поверхность будет равен нулю:
$$
\oint_S {(D\cdot N)}dS = \iint{\operatorname{div}DdV} = 0 \qquad (3)
$$
Если записать поток поля через клетку и приравнять к нулю, то получится уравнение Лапласа:

$$
\frac{\partial^2 \varphi}{\partial x^2} + \frac{\partial^2 \varphi}{\partial y^2} = 0 \qquad (4)
$$
Используя это уравнение можно получить выражение для потенциала в точке с координатами \(x\) и \(y\):

Имея (5), можно итерационно просчитывать потенциал для всей решётки (можно показать, что такой метод вычисления потенциала быстро сходится к правильному результату). Осталось придумать правило для роста так называемого стримера. Принцип моделирования стримера я нашёл в книжке "Д. А. Медведев, А. Л. Куперштох, Э. Р. Прууэл, Н. П. Сатонкина, Д. И. Карпов - Моделирование физических процессов и явлений на ПК."
Мы рассмотрим один из самых простых критериев роста, а именно модель НПВ: Нимейером, Пьетронеро и Висманом впервые была предложена модель, которая позволяет описать рост структур разряда в диэлектриках. В основе модели лежит предположение, что структура растет случайным образом, причем вероятность роста зависит только от локального электрического поля вблизи структуры.
Для расчета электрического поля в диэлектрике область моделирования покрывается сеткой (например, квадратной в двумерном случае или кубической — в трехмерном), на которой решается уравнение Лапласа. Рост начинается с одной из точек на электроде. На каждом шаге роста с некоторой вероятностью может образоваться одна веточка разрядной структуры. Эта веточка будет соединять два соседних узла сетки, один из которых уже принадлежит разрядной структуре, а другой является «диэлектриком».

Таким образом, из каждого узла двумерной сетки может образоваться до восьми веточек, если учитывать возможность роста и по диагоналям (для трехмерной сетки до 26 веточек). Мы учтём только 4 направления. Пусть \(E\) — среднее значение проекции электрического поля на направление, соединяющего два соседних узла сетки, между которыми может образоваться новая ветвь разрядной структуры. Обычно предполагают, что вероятность ее образования приближенно равна \(p(E) = E^{\eta}\) где \(\eta\) — так называемый показатель роста, зависящий только от свойств диэлектрика. На каждом шаге роста случайный процесс выбора новой веточки структуры реализуется следующим алгоритмом. Пробегаем по всем \(M\) узлам решетки, в которые возможен рост, и рассчитываем сумму:

$$
Z = \sum\limits_{i=1}^M{E_k^{\eta}} \qquad (6)
$$
где величина \(E_k\) — своя для каждой пары узлов и находится на каждом шаге роста по текущему распределению электрического поля. Затем разыгрывается случайное число \(\psi\) , равномерно распределенное от 0 до \(Z\). Для этого используется формула \(\psi = Z \cdot random()\). Затем повторно шаг за шагом рассчитывается (6) до тех пор, пока текущая сумма \(\Sigma{E_k^{\eta}}\) не станет больше \(\psi\). Тот узел, для которого сумма стала больше \(\psi\), присоединяется к структуре. Новой образовавшейся веточке присваивается значение потенциала того электрода, с которого начался рост этого стримера, после этого идет итерационный пересчет поля с помощью (5). Таким образом формируется эквипотенциальная структура:

Такая модель роста принадлежит к классу однозвенных моделей, в которых считается, что проводящее звено, появившееся первым, подавляет рост остальных на текущем временном шаге.
При увеличении \(\eta\) уменьшается ветвистость структуры:

Фрактальная размерность коронного разряда \( D \approx 2.16 \) - немного больше, чем размерность траектории броуновского движения.

Фракталы в жизни встречаются очень часто, что впервые заметил Бенуа Мандельброт, написавший книгу "The Fractal Geometry of Nature". В ней есть описание того, как можно моделировать большое множество всяких интересных вещей из реальной жизни, которые на первый взгляд кажутся сложными и не понятными.

Друзья! Я очень благодарен вам за то, что вы интересуетесь моими работами, ведь каждый пост на сайте даётся очень непросто. Я буду рад любому отклику и поддержке с вашей стороны.