Нейронные сети. (Machine learning #1)

Что такое нейронная сеть и как она работает? Разбираем популярную технологию на простых примерах!
Сайту исполняется год и в честь этого я решил написать небольшой пост о том, чем я сейчас занимаюсь :)

Кстати, у меня есть замечательная школа математики для программистов – Академия вектозавров. Первую, бесплатную, главу пройти обязательно всем! :)

Однажды, гуляя по просторам YouTube, я наткнулся на очень классный канал, посвященный математике, физике и многим другим интересным вещам (даже радиоэлектронике!) На канале было очень много всего, чего я не успел пока посмотреть, но я обратил внимание на ролик, посвященный работе нейронных сетей. Так как я давно уже слышал о нейронных сетях и похожих вещах (вроде генетических алгоритмов), но при этом не понимал толком, о чём идёт речь, я очень заинтересовался. Это цикл из 4х видео, которые, по сути, являются визуализацией статьи Michael Nielsen.



Здесь я хочу дать краткое и простое описание работы нейронной сети на примере классической задачи распознавания нарисованных от руки цифр.
Итак, представьте, что перед вами встала задача распознать цифры:

Наш мозг без труда справляется с такой задачей! Но что, если у нас есть миллион написанных от руки цифр, которые необходимо распознать и записать, допустим, в базу данных. Нужно написать программу, которая будет делать это за вас.
Но как будет работать такая программа? И тут задача, которая казалась пустяковой, превратилась в большую проблему: каждый человек пишет одни и те же цифры по-разному, а компьютер этого не знает. Вот, например, написанная по-разному, цифра 5:

Нам без проблем удаётся определить, что это одна и та же цифра, но как мы это делаем? Дело в том, что мы смотрим не на каждый отдельный пиксель, а на общую картину. Количество закорючек, петель, углов и т.д - мозг, сверяя все эти детали с тем, что мы до этого видели и узнали, понимает, что перед нами один и тот же объект - цифра 5:

Нейронная сеть работает точно так же: программист не обязан "учить" сеть, как распознавать и что конкретно сравнивать - компьютер делает это сам! Необходимо только "натренировать" его, давая на распознавание картинки цифр и ответы (чем-то похоже на ученика, который готовится к ЕГЭ). То есть перед тем, как алгоритм сможет работать, ему нужно "показать" большое количество примеров:

Понятие нейрона, веса и смещения

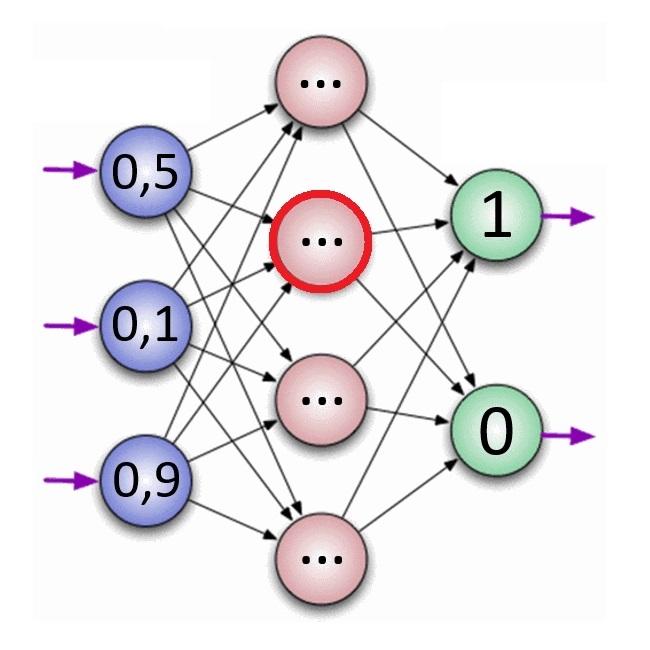
Давайте рассмотрим простую нейронную сеть:

Эта нейронная сеть состоит из входного слоя, в котором 3 нейрона, одного скрытого слоя, в котором 4 нейрона и выходного слоя, в котором 2 нейрона.
Количество скрытых слоёв и нейронов в каждом слое может варьироваться.
Внутри каждого нейрона записано число \( x \) от 0 до 1. То есть нейрон - это просто число от нуля до единицы, не более. Каждый нейрон из одного слоя влияет на каждый нейрон из следующего.
Как записать эту связь? Рассмотрим один нейрон из скрытого слоя (выделен красным): он связан с нейронами из предыдущего слоя (в данном случае это входной слой). Каждый нейрон из входного слоя даёт свой вклад в то число, которое получится в рассматриваемом нейроне. Некоторые нейроны дают большой вклад, а некоторые - совсем маленький. Вклад определяется умножением на некоторое число \( w \), которое назовём весом нейрона (weight):

Запишем сумму со всех нейронов из входного слоя:

$$
z = \sum\limits_{i=1}^{3}{x_i w_i} \qquad (1)
$$
Получившийся результат может быть любым вещественным числом. Нам нужно преобразовать его в число от 0 до 1, которое мы и присвоим нейрону.
Сделать это можно, например, так:

$$
\sigma(z) = \frac{1}{1 + e^{-z}} \qquad (2)
$$
Формула может показаться сложной, но это нет так.
Рассмотрим и проанализируем её: если \(z \) очень большое, то экспонента в знаменателе зануляется и ответом будет 1. Если \(z \) - очень большое отрицательное число, то знаменатель увеличивается и ответ \(= 0\). Мы получили именно то, что нам нужно!
График функции \(\sigma(z)\):

Видно, что рост функции от нуля до единицы происходит в окрестности нуля. Но часто активационный барьер необходимо сместить. Поэтому к числу \(z \) в (1) нужно прибавить число \(b \), которое называется смещением (bias). То есть

$$
z = \sum\limits_{i=1}^{n}{x_i w_i} + b \qquad (3)
$$
Для всего слоя (в матричном виде):

$$
\begin{pmatrix}
z_1 \\
z_2 \\
z_3 \\
... \\
z_n
\end{pmatrix}
=
\begin{bmatrix}
w_1^1 & w_1^2 & w_1^3 & ... & w_1^m \\
w_2^1 & w_2^2 & w_2^3 & ... & w_2^m \\
w_3^1 & w_3^2 & w_3^3 & ... & w_3^m \\
...\\
w_n^1 & w_n^2 & w_n^3 & ... & w_n^m \\
\end{bmatrix}
\begin{pmatrix}
x_1 \\
x_2 \\
x_3 \\
... \\
x_m
\end{pmatrix}
+
\begin{pmatrix}
p_1 \\
p_2 \\
p_3 \\
... \\
p_n
\end{pmatrix} \qquad (4)
$$
И новые нейроны получаются применением сигмойды (2) к (4):

$$
\begin{pmatrix}
y_1 \\
y_2 \\
y_3 \\
... \\
y_n
\end{pmatrix}
=
\begin{pmatrix}
\sigma(z_1) \\
\sigma(z_2) \\
\sigma(z_3) \\
... \\
\sigma(z_n)
\end{pmatrix} \qquad (5)
$$
Так, последовательно применяя (4) и (5) к каждому слою, мы придём к выходному, который и будет результатом работы алгоритма.
Резюмируя написанное выше, можно сказать, что нейронная сеть - это просто набор чисел, условно разделённых слоями (взаимосвязями): нейроны (\(x_i\)), веса (\(w_i\)) и смещения (\(p\)). Все слои, начиная с входного, последовательно вычисляются по правилу (5). То есть все нейроны (числа внутри кружков) определяются нейронами из входного слоя, смещениями и весами.

Как происходит обучение?

Вернёмся к задаче определения нарисованных цифр. Входной слой нейронов можно определить следующим образом: смотрим на каждый пиксель и переводим его оттенок в число от нуля до единицы. Чем светлее пиксель, тем число ближе к нулю, чем темнее - к единице.

Картинка \(28*28 \) содержит \(784 \) пикселя, именно столько и будет нейронов в входном слое.
В выходном слое будет 10 нейронов, каждый из которых указывает на цифру от \(0\) до \(9\). Для упрощения понимания изобразим лишь один скрытый слой. По выходному слою мы будем судить о том, как отработал алгоритм.

Как и было сказано ранее, работа алгоритма полностью определяется входными данными и взаимосвязями нейронов. Когда алгоритм не натренирован, то, скорее всего, он не сможет дать правильный ответ, так как взаимосвязи между нейронами (веса нейронов и смещения) настроены неправильно. Именно в подборе этих параметров и заключается обучение нейронной сети.
Теперь дадим нашей сети группу картинок с написанными цифрами для тренировки и после каждого завершения алгоритма будем проверять то, насколько точно она "угадала" цифру.
Для того, чтобы оценить эффективность работы алгоритма, введём так называемую функцию расходимости (cost function) следующим образом:

$$
C(w, b) \equiv \frac{1}{2l}\sum\limits_{x_{in}}{||y(x_{in}) - a||^2} \qquad (6)
$$
Где \(l\) - это общее количество тренировочных входных слоёв;
\(x_{in}\) - это входной слой нейронов;
\(y(x_{in})\) - это выходной слой (результат работы);
\(a\) - это "правильный" выходной слой, т.е это правильные ответы.

Чем ближе результат работы алгоритма к требуемому результату, тем меньше становится функция расхождения. То есть задача обучения на данном этапе сводится к уменьшению функции расхождения.
Как нужно изменять все \(w\) и \(b\), чтобы максимально быстро уменьшить функцию расхождения?
Нужно найти вектор-градиент функции и идти в противоположную сторону. Если бы наша сеть имела только одно смещение \(b\) и один вес \(w\), то данный процесс можно было бы проиллюстрировать мячом, скатывающимся в самую нижнюю точку ямки:

$$
\nabla{C(w, b)} = \left( \frac{\partial C(w, b)}{\partial w_1}; ... \frac{\partial C(w, b)}{\partial w_s}; \frac{\partial C(w, b)}{\partial b_1}; ... \frac{\partial C(w, b)}{\partial b_k} \right)\qquad (7)
$$
Где \(s\) - это общее количество весов. То есть \(s\) - это общее количество связей. Важно отметить, что это очень большое число: в сети, показанной выше, \(784\) входных нейрона, которые связаны с \(15\) нейронами из скрытого слоя - всего \(11760\) связей \(+\) каждый из \(15\) нейронов связан с \(10\) нейронами выходного слоя - это ещё \(150\) связей. В итоге \(s = 11910\);
\(k\) - это количество смещений, которое равно количеству нейронов (не считая входного слоя). В нашем случае \(k = 809\).
Теперь остался небольшой шаг - найти все частные производные. Делается это по цепному правилу:

$$
\frac{\partial C(w, b)}{\partial w_i} = \sum\limits_{t=1}^{n}{\frac{\partial C(w, b)}{\partial y_t}\frac{\partial y_t(x_{in}, w, b)}{\partial w_i}}
$$
Используя определение (6):

$$
\frac{\partial C(w, b)}{\partial y_t} = \frac{1}{2l}2y_t = \frac{y_t}{l}
$$
А производная
$$
\frac{\partial y_t(x_{in}, w, b)}{\partial w_i}
$$
легко считается, так как у нас есть явный вид функции \(y_t\) от \(w_i\) в (5).
Теперь разберёмся с производными \(С(w, b)\) по смещениям \(b\). Расчёт производится аналогично:

$$
\frac{\partial C(w, b)}{\partial b_i} = \sum\limits_{t=1}^{n}{\frac{\partial C(w, b)}{\partial y_t}\frac{\partial y_t(x_{in}, w, b)}{\partial b_i}}
$$
Где
$$
\frac{\partial y_t(x_{in}, w, b)}{\partial b_i}
$$
легко считается, используя связь в (5).

В принципе, это все! Весь процесс обучения взял на себя компьютер, который считает частные производные функции расхождения и с их помощью правильно корректирует параметры связей нейронов.
Однако, как я понял, чаще всего вычисляют не все частные производные (в нашем случае их \(12719\)), а только часть, разделяя параметры на небольшие группы. Такой подход называется stochastic gradient descent, и он быстрее приводит к нужному результату, так как на вычисление всех частных производных тратится большее время.

Можете похлопать себя по плечам, ведь выше прочитанный материал не из простых и требует усилия для усвоения!
Это не последний мой пост, посвященный нейронным сетям и машинному обучению. У меня есть несколько крутых проектов, связанных с этой темой, которые я хочу реализовать и более глубоко раскрыть в следующих моих статьях.

Отдельная благодарность моей сестре Соне (отличному репетитору по русскому языку) за час смеха и мучения при правке статьи!

Друзья! Я очень благодарен вам за то, что вы интересуетесь моими работами, ведь каждый пост на сайте даётся очень непросто. Я буду рад любому отклику и поддержке с вашей стороны.