Как делаются красивые цветные графики и диаграммы?

Сегодня я расскажу о том, как можно сделать цветные диаграммы или графики. По сути, это просто трехмерные графики в двумерном виде.

Кстати, у меня есть замечательная школа математики для программистов – Академия вектозавров. Первую, бесплатную, главу пройти обязательно всем! :)

Недавно я моделировал электрическое поле от заряда и мне хотелось наглядно и красиво показать цветом величину потенциала в точке. С этой задачей я уже давно сталкивался, но решал её не очень красиво. Моя реализация была плоха тем, что использовался только один цвет. То есть была функция, которая принимает число от нуля до единицы и возвращает оттенок серого. Чем ближе параметр к единице, тем более черный цвет она отдает на выход. При таком подходе не всегда удаётся четко показать границы важных областей. В некоторых языках ещё есть функция интерполяции одного цвета в другой, что по сути есть то же самое.

А мне хотелось добиться примерно такого результата:

Видно, что здесь используются все цвета радуги и выглядит это очень красиво. В общем, решил я сам написать функцию, которая возвращала бы цвет в зависимости от параметра на входе.

Способ представления цвета. Система RGB и HEX

Начнём с того, как мы будем представлять цвет. Самыми популярными форматами хранения цветов является RGB (Red, Green, Blue) и HTML таблица цветов. Нам будет удобнее работать с форматом RGB. RGB – это аддитивная модель хранения цвета с помощью трех основных цветов. Выбор основных цветов, вообще то говоря, произвольный. Красный, зелёный и желтый выбраны из-за наших особенностей восприятия цвета. На каждый цвет приходится по одному байту (число от \(0\) до \(255\)). С помощью \(3\)х байт таким способом удастся закодировать \(256*256*256 = 16777216\) цветов! Такого количества оттенков хватает с головой для любых целей.

По сути, цвета в RGB – это трёхмерные векторы:

$$
Color = [a_1, a_2, a_3]
$$
Где \(a_1, a_2\) и \(a_3\) – это оттенки красного, зелёного и синего цветов соответственно, суть числа от \(0\) до \(255\).
HTML таблица цветов предлагает способ хранения в виде шестнадцатеричных чисел. Между цветами одной системы и другой есть правило перевода (Существует биективное отображение).

Принцип сопоставления цветов с числами

Нам нужен такой алгоритм, который бы принимал число от нуля до единицы (нормированный параметр), а возвращал соответствующий цвет. Для того, чтобы понять, как построить такой алгоритм нужно просто посмотреть на весь спектр цветов и понять, как меняются числа \(a_1, a_2\) и \(a_3\):

Видно, что чтобы пройтись по всем цветам нужно поочередно непрерывно изменять компоненты \([a_1, a_2, a_3]\) вектора цвета.

В зависимости от того, какой параметр дан на вход возвращаем нужный цвет:

function color_interpolate(progress) {

	var result_color = [0, 0, 255]; // Вектор цвета RGB

	

	if((progress <= 0) || (progress >= 1)) // Случаи, когда параметр меньше 0 или больше 1

		return (progress <= 0) ? "rgb(0,0,255)" : "rgb(255,0,0)";



	if(progress < 0.25) // Синий -> Голубой

		result_color = [0, (progress/0.25)*255, 255];

	else if(progress < 0.5) // Голубой -> Зелёный

		result_color = [0, 255, 255*(1-(progress-0.25)/0.25)];

	else if(progress < 0.75) // Зелёный -> Жёлтый

		result_color = [255*(progress-0.5)/0.25, 255, 0];

	else // Жёлтый -> Красный

		result_color = [255, 255*(1-(progress-0.75)/0.25), 0];



	return "rgb(" + result_color[0]

				  + "," + result_color[1]

				  + "," + result_color[2] + ")"; // Возвращаем готовый цвет

}

Можно уменьшить функцию color_interpolate, если последовательно изменять цвет - начнем с синего цвета и доберёмся до нужного:

function color_interpolate(progress) {

	var result_color = [0, 0, 255]; 



	if((progress <= 0) || (progress >= 1))

		return (progress <= 0) ? "rgb(0,0,255)" : "rgb(255,0,0)";



	for(var i = 0; progress > (i+1)/4; i++)

		result_color[(i+1)%3] = (i%2 == 0) ? 255 : 0;

	

	result_color[(i+1)%3] = (i%2 == 0) ? (4*progress - i)*255 : (1 + i-4*progress)*255;

	return "rgb(" + result_color[0]

				  + "," + result_color[1]

				  + "," + result_color[2] + ")";

}

То же самое, но на C++:

std::vector<int> colorInterpolate(double progress) {

    std::vector<int> result_color = {0, 0, 255};

    if((progress <= 0) || (progress >= 1))

        return (progress <= 0) ? result_color : std::vector<int>{255,0,0};

    int i = 0;

    for(i = 0; progress > (double)(i+1)/4; i++)

        result_color[(i+1)%3] = (i%2 == 0) ? 255 : 0;

    result_color[(i+1)%3] = (i%2 == 0) ? (4*progress - i)*255 : (1 + i-4*progress)*255;



    return result_color;

}

Теперь протестируем полученную функцию на примерах.

Примеры использования

Для начала построим графики некоторых функций.
Функция
$$
z = x+y
$$
будет выглядеть следующим образом:

Как и следовало ожидать мы получили простой градиент.
Попробуем что-нибудь поинтереснее:

$$
z = cos\left(\frac{10x}{y}\right)
$$

$$
z = cos(sin(cos(xy)y))
$$

$$
z = cos(x sin(y cos(xy)))
$$

$$
z = sin\left(\frac{x}{y}\right) sin\left(\frac{y}{x}\right)
$$

$$
z = sin(x) + sin(y)
$$

$$
z = sin(x) cos(sin(x) y)
$$

$$
z = \frac{sin(x)}{sin(y)}
$$

Кулоновский потенциал заряда выражается следующим образом:

$$
\varphi = \frac{q}{r}
$$
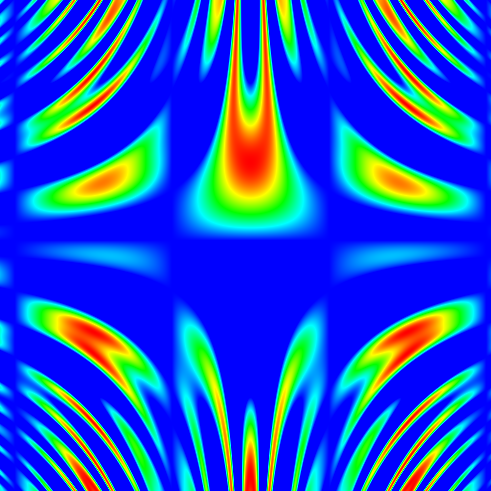
Имея распределение зарядов можно посчитать потенциал во всех точках:

Черными линиями обозначены направления электрического поля (силовые линии). Если проводить замкнутые кривые, перпендикулярные силовым линиям в каждой точке, мы получим так называемые эквипотенциали (линии вдоль которых потенциал не меняется, а значит цвет остаётся постоянным)

Друзья! Я очень благодарен вам за то, что вы интересуетесь моими работами, ведь каждый пост на сайте даётся очень непросто. Я буду рад любому отклику и поддержке с вашей стороны.